Skip to article frontmatterSkip to article content

In this lesson, we’ll learn how to evaluate the quality of a machine learning model. By the end of this lesson, students will be able to:

  • Apply get_dummies to represent categorical features as one or more dummy variables.
  • Apply train_test_split to randomly split a dataset into a training set and test set.
  • Evaluate machine learning models in terms of overfit and underfit.
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

import pandas as pd

Dummy variables

Last time, we tried to predict the price of a home from all the other variables. However, we learned that since the city column contains categorical string values, we can’t use it as a feature in a regression algorithm.

homes = pd.read_csv("homes.csv")
homes

This problem not only occurs when using DecisionTreeRegressor, but it also occurs when using LinearRegression since we can’t multiply a categorical string value with a numeric slope value. Let’s learn how to represent these categorical features as one or more dummy variables.

def model_parameters(reg, columns):
    """Returns a string with the linear regression model parameters for the given column names."""
    slopes = [f"{coef:.2f}({columns[i]})" for i, coef in enumerate(reg.coef_)]
    return " + ".join([f"{reg.intercept_:.2f}"] + slopes)
X = homes.drop("price", axis=1)
y = homes["price"]
reg = LinearRegression().fit(X, y)

print("Model:", model_parameters(reg, X.columns))
print("Error:", mean_squared_error(y, reg.predict(X)))

Overfitting

In our introduction to machine learning, we explained that the researchers who worked on calibrating the PurpleAir Sensor (PAS) measurements against the EPA Air Quality Sensor (AQS) measurements ultimately decided to use the model that included only the PAS and humidity features (variables)—ignoring the opportunity to use the temperature and dew point even though a model that includes all features produced a lower overall mean squared error.

sensor_data = pd.read_csv("sensor_data.csv")
sensor_data
from sklearn.metrics import root_mean_squared_error

X = sensor_data.drop("AQS", axis=1)
y = sensor_data["AQS"]
reg = LinearRegression().fit(X, y)

print("Model:", model_parameters(reg, X.columns))
# RMSE, or root mean squared error, is the square root of the mean of the squared errors.
print("Error:", root_mean_squared_error(y, reg.predict(X)))

In fact, the authors (Barkjohn et al. 2021) tested the impact of incrementally introducing a feature to the model to determine which combination of features could provide the most useful model—not necessarily the most accurate one. In their research, they aimed to predict the PAS measurement from the AQS measurement, the opposite of our task, and they included interactions between features indicated by the × symbol. For each grouping of models with a certain number of features, they highlighted the model with the lowest root mean squared error (RMSE, or the square root of the MSE) using an asterisk *.

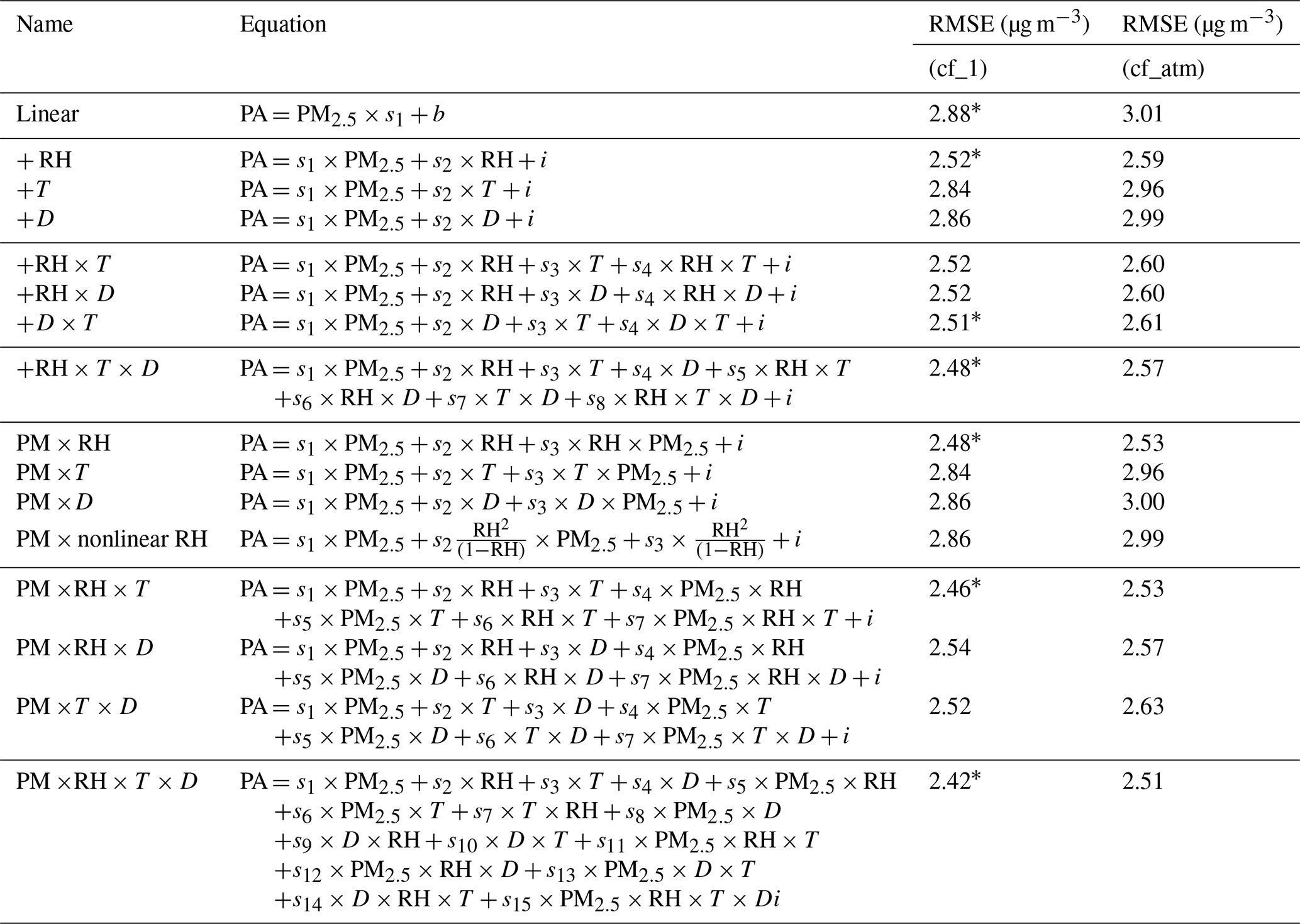
Table 2 from Barkjohn et al. 2021 depicting every combination of features used in linear models

The model at the bottom of the table that includes all the features also has the lowest RMSE loss. But the loss value alone is not a convincing measure: adding more features into a model not only leads to a model that is harder to explain, but also increases the possibility of overfitting.

A model is considered overfit if its predictions correspond too closely to the training dataset such that improvements reported on the training dataset are not reflected when the model is run on a testing dataset (or in the real world). To simulate training and testing datasets, we can take our X features and y labels and subdivide them into X_train, X_test, y_train, y_test using the train_test_split function. The testing dataset should only be used during final model evaluation when we’re ready to report the overall effectiveness of our final machine learning model.

from sklearn.model_selection import train_test_split

# test_size=0.2 indicates 80% training dataset and 20% testing dataset
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# During model training, use only the training dataset
reg = LinearRegression().fit(X_train, y_train)

print("Model:", model_parameters(reg, X_train.columns))
print("Error:", root_mean_squared_error(y_test, reg.predict(X_test)))

Feature selection

Feature selection describes the process of selecting only a subset of features in order to improve the quality of a machine learning model. In the air quality sensor calibration study, we can begin with all the features and gradually remove the least-important features one-by-one.

features = ["PAS", "humidity", "temp", "dew"]

reg = LinearRegression().fit(X_train.loc[:, features], y_train)
print("Model:", model_parameters(reg, features))
print("Error:", root_mean_squared_error(y_test, reg.predict(X_test.loc[:, features])))

Recursive feature elimination (RFE) automates this process by starting with a model that includes all the variables and removes features from the model starting with the ones that contribute the least weight (smallest coefficients in a linear regression).

from sklearn.feature_selection import RFE

# Remove 1 feature per step until half the original features remain
rfe = RFE(LinearRegression(), step=1, n_features_to_select=0.5, verbose=1)
rfe.fit(X_train, y_train)

# Show the final subset of features
rfe_features = X.columns[[r == 1 for r in rfe.ranking_]]
print("Features:", list(rfe_features))

# Extract the last LinearRegression model trained on the final subset of features
reg = rfe.estimator_

print("Model:", model_parameters(reg, rfe_features))
print("Error:", root_mean_squared_error(y_test, rfe.predict(X_test)))

Cross validation

How do we know when to stop removing features during feature selection? We can certainly use intuition or look at the changes in error as we remove each feature. But this still requires us to evaluate the model somehow. If the testing dataset can only be used at the end of model evaluation, it was wrong of us to use the testing dataset during feature selection!

Cross-validation provides one way to help us explore different models before we choose a final model for evaluation at the end. Cross-validation lets us evaluate models without touching the testing dataset by introducing new validation datasets.

The simplest way to cross-validate is to call the cross_val_score helper function on an unfitted machine learning algorithm and the dataset. This function will further subdivide the training dataset into 5 folds and, for each of the 5 folds, train a separate model on the training folds and evaluate them on the validation fold.

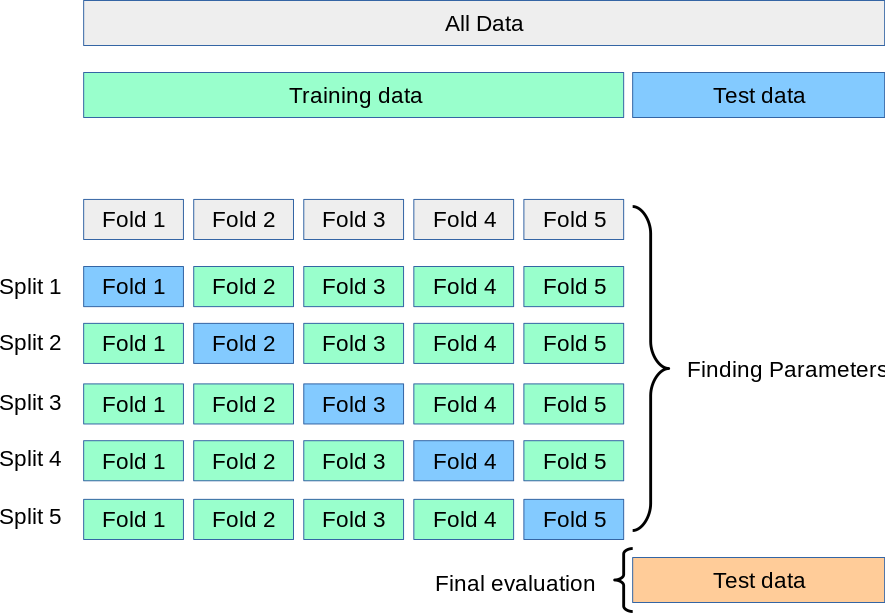
A depiction of a 5 fold cross validation on a training set, while holding out a test set

The scoring parameter can accept the string name of a scorer function. Higher (more positive) scores are considered better, so we use the negative RMSE value as the scorer function.

from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeRegressor

cross_val_score(
    estimator=DecisionTreeRegressor(max_depth=2),
    X=X_train,
    y=y_train,
    scoring="neg_root_mean_squared_error",
    verbose=3,
)

As we’ve seen throughout these lessons on machine learning, we prefer to automate our processes. Rather than modify the max_depth and manually tweaking the values until we find something that works, we can use GridSearchCV to exhaustively search all hyperparameter options. Here, the first 5 folds for max_depth=2 are exactly the same as cross_val_score.

from sklearn.model_selection import GridSearchCV

search = GridSearchCV(
    estimator=DecisionTreeRegressor(),
    param_grid={"max_depth": [2, 3, 4, 5, 6, 7, 8, 9, 10]},
    scoring="neg_root_mean_squared_error",
    verbose=3,
)
search.fit(X_train, y_train)

# Show the best score and best estimator at the end of hyperparameter search
print("Mean score for best model:", search.best_score_)
reg = search.best_estimator_
print("Best model:", reg)

Finally, we can report the test error for the best model by evaluating it against the testing dataset. Why is the testing dataset error different from the mean score for the best model printed above?

print("Error:", root_mean_squared_error(y_test, reg.predict(X_test)))

Visualizing decision tree models

Last time, we plotted the predictions for a linear regression model that was trained to take PAS measurements and predict AQS measurements. What do you think a decision tree model would look like for this simplified PurpleAir sensor calibration problem?

Here’s a complete workflow for decision tree model evaluation using the practices above. The resulting plot compares a linear regression model lmplot against the decisions made by a decision tree.

# Split dataset into 80% training dataset and 20% testing dataset
X = sensor_data.drop("AQS", axis=1)
y = sensor_data["AQS"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# Recursive feature elimination to select the single most important feature based on slope value
rfe = RFE(LinearRegression(), n_features_to_select=1, verbose=1)
rfe.fit(X_train, y_train)
# Print the best feature to predict AQS
rfe_feature = X.columns[rfe.ranking_.argmin()]
print("Best feature to predict AQS:", rfe_feature)
# Use only the best feature
X = X[[rfe_feature]]
X_train = X_train[[rfe_feature]]
X_test = X_test[[rfe_feature]]

# Grid search cross-validation to tune the max_depth hyperparameter using RMSE loss metric
search = GridSearchCV(
    estimator=DecisionTreeRegressor(),
    param_grid={"max_depth": [2, 3, 4, 5, 6, 7, 8, 9, 10]},
    scoring="neg_root_mean_squared_error",
    verbose=3,
)
search.fit(X_train, y_train)
# Print the best score and best estimator at the end of hyperparameter search
print("Mean score for best model:", search.best_score_)
reg = search.best_estimator_
print("Best model:", reg)

# During model evaluation, use the testing dataset
print("Test error:", root_mean_squared_error(y_test, search.predict(X_test)))

# Visualize the tree decisions compared to a LinearRegression model (lmplot)
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn.tree import plot_tree
sns.set_theme()
grid = sns.lmplot(sensor_data, x=rfe_feature, y="AQS")
# Create a demonstration dataset that counts from 0 to the max PAS value
X_demo = pd.DataFrame(np.arange(X[rfe_feature].max()), columns=[rfe_feature])
grid.facet_axis(0, 0).plot(X_demo, reg.predict(X_demo), c="orange", linewidth=3)
grid.set(title=f"lmplot vs {reg}")
# Show nodes in the decision tree
plt.figure(dpi=300)
plot_tree(
    reg,
    max_depth=2, # Only show the first two levels
    feature_names=[rfe_feature],
    label="root",
    filled=True,
    impurity=False,
    proportion=True,
    rounded=False
);

The testing dataset error rates for both the DecisionTreeRegressor and the LinearRegression models are not too far apart. Which model would you prefer to use? Justify your answer using either the error rates below or the visualizations above.

print("Tree error:", root_mean_squared_error(y_test, search.predict(X_test)))
print("Line error:", root_mean_squared_error(
    y_test,
    LinearRegression().fit(X_train, y_train).predict(X_test),
))

Earlier, we discussed how overfitting to the testing dataset can be mitigated by using cross-validation. But in answering the previous question on whether we should prefer a DecisionTreeRegressor model or a LinearRegression model, we’ve actually overfit the model by hand! Explain how preferring one model over the other according to the visualization overfits to the testing dataset.

References
  1. Barkjohn, K. K., Gantt, B., & Clements, A. L. (2021). Development and application of a United States-wide correction for PM2.5 data collected with the PurpleAir sensor. Atmospheric Measurement Techniques, 14(6), 4617–4637. 10.5194/amt-14-4617-2021
Lectures
Learning Algorithms
Lectures
Bias, Variance, Bias, and Bias